Grupos: figuras 1, 2 y 3

En matemáticas un grupo está formado por un conjunto de elementos, incluyendo un elemento neutro y un elemento recíproco para cada elemento, y una operación. La operación toma dos elementos cualesquiera para dar otro elemento del conjunto. La figura 1 ilustra cinco de los seis elementos que, junto con el elemento neutro e, transforman un triángulo equilátero en sí mismo: r1 gira el triángulo 120º, r2 lo gira 240º, y f1, f2 y f3 voltean al triángulo alrededor de las rectas L1, L2 y L3 respectivamente. Las figuras 2 y 3 muestran cómo al aplicar f2 y después r1 a un triángulo equilátero el efecto es idéntico a aplicar sólo f1.

Dibujo vectorial

Dibujo vectorial

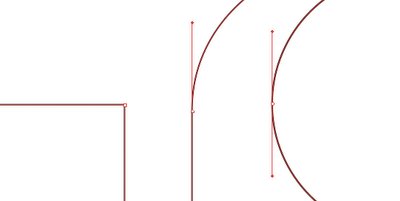Los diseñadores le tienen terror al dibujo vectorial de precisión. Muchos tienen bellísimos bocetos de logotipos o tipografías, pero su inseguridad con el trazo o la mala realización del dibujo vectorial despotencia la belleza de sus diseños. En fin, un grupo de diseñadores propone un sistema de dibujo con los controladores organizados de manera ortogonal, ¿pero hasta qué punto puede ser la mejor solución?. Analizaremos las características que debe poseer un dibujo vectorial perfecto.
Existen 3 tipos de puntos: el de esquina, el de curva y el de semicurva o tangencial. Los controladores pueden estar dispuestos de tres maneras, enganchados, independientes o sin ellos.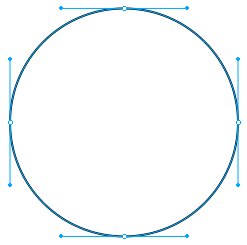
Parece obvio, obvio.
Pero, ¿dónde se ubican los puntos?
En un principio, ubicaremos los puntos de manera ortogonal, y en el extremo del eje. Como vemos en el ejemplo, tanto los controladores como los puntos confluyen hacia un centro en común.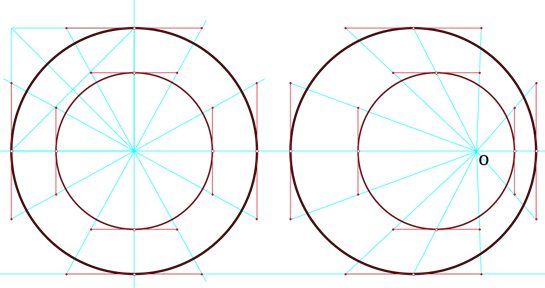Complejicemos un poco más el esquema y nos daremos cuenta de algo sorprendente: el modelo es totalmente adaptable, y las curvas externas por lo general tienen absoluta relación con las curvas internas y viceversa, así como también los controladores. El primer ejemplo de arriba parece pecar de tonto y simple, pero no lo es tanto, podemos darnos cuenta cómo están dispuestos los controladores en un círculo perfecto (30 grados con respecto al centro), y como se complementa el círculo interno con el externo (podemos dibujar 1000 circulos más concéntricos y siempre será lo mismo.
En el segundo ejemplo (de arriba), podemos observar cómo se mantiene este mismo principio, en un círculo perfecto desfasado. Para muchos aprender esto esto puede resultar inútil, pero no lo es tanto, ya que si miramos la mitad de abajo de este ejemplo, puede ser fácilmente la mitad de abajo de una letra "U" mayúscula serif.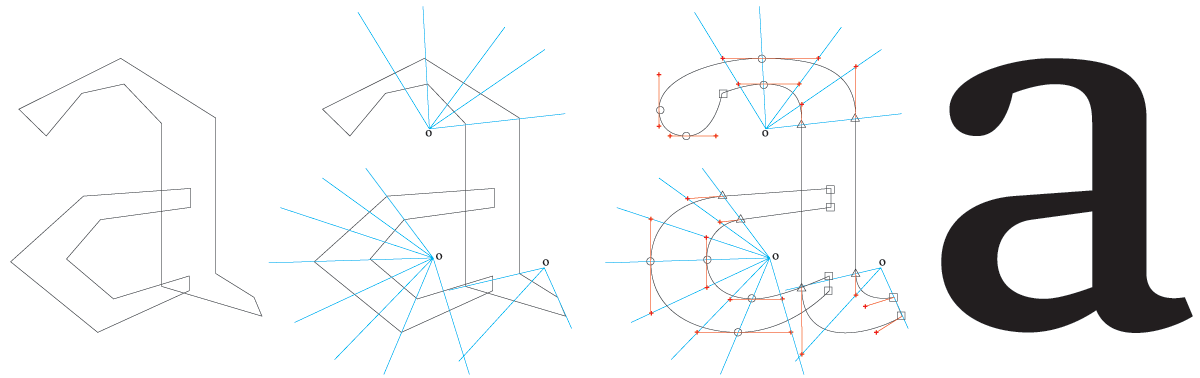En este último ejemplo, podemos ver una aplicación de lo anterior, donde no tan sólo la forma está muy bien dibujada, sino fíjense en las contraformas, sus curvas se ven claras y perfectas.

Perspectiva cónica

Saltar a navegación, búsqueda

La perspectiva cónica es un sistema de representación gráfico basado en la proyección de un cuerpo tridimensional sobre un plano auxiliándose en rectas proyectantes que pasan por un punto. El resultado se aproxima a la visión obtenida si el ojo estuviera situado en dicho punto.

Filippo Brunelleschi fue el primero que formula las leyes de la perspectiva cónica, mostrando en sus dibujos las construcciones en planta y alzado, indicando las líneas de fuga.

Perspectiva caballera

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

La perspectiva caballera es un sistema de proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.

Perspectiva caballera. La semicircunferencia paralela al plano frontal está en verdadera magnitud (sin sufrir deformaciones).

En perspectiva caballera, dos dimensiones del volumen a representar se proyectan en verdadera magnitud y la tercera con un coeficiente de reducción. Las dos dimensiones sin distorsión angular con sus longitudes a escala son la anchura y altura (x, y) mientras que la dimensión que refleja la profundidad (z) se reduce en una proporción 1:2.

Los ejes X e Y forman un ángulo de 90º, y el eje Z suele tener 45º (o 135º) respecto ambos.

Se puede dibujar fácilmente un volumen a partir de una vista lateral o alzado, trazando a partir de cada vértice líneas paralelas a Z, para reflejar la profundidad del volumen.

Este tipo de proyección es frecuentemente utilizada por su facilidad de ejecución, aunque el resultado final no da una imagen tan real como la que se obtendría con una proyección cónica.

PERSPECTIVA DIMETRICA

La perspectiva dímétrica es una herramienta del Dibujo Técnico, que forma parte a su vez de la Axonometría, para representar volúmenes.
El dibujo parte de dos ángulos con la misma amplitud y otro ángulo de amplitud diferente para formar los tres ejes que se utilizan para el trazado del objeto. Los ángulos más usuales para esta perspectiva son 105° y 150°. Esta perspectiva, o proyección es usual para representar piezas más largas que anchas y altas.

La perspectiva isométrica

-En la perspectiva isométrica, el espacio se estructura igual que en la perspectiva caballera, por medio de tres ejes coordenados perpendiculares entre sí. Pero, al contrario que en la caballera, no se sitúa en el plano del papel ninguna de las caras del objeto a representar.

- Orientación de los ejes en la perspectiva isométrica
Para comenzar, situamos los ejes coordenados. El eje OX, formando un ángulo de 30° con la horizontal, hacia la derecha. El eje OY, formando un ángulo de 30° con la horizontal,...

- Perspectiva isométrica con papel reticulado
En ocasiones puede resultar útil emplear un papel con retícula para situar las aristas del objeto representado en perspectiva isométrica. Observemos esta figura:. El papel reticulado...

PERSPECTIVA AXONOMETRICA

La perspectiva axonométrica es un sistema de representación gráfica, consistente en representar elementos geométricos o volúmenes en un plano, mediante proyección ortogonal, referida a tres ejes ortogonales, de tal forma que conserven su proporciones en las tres direcciones del espacio: altura, anchura y longitud.

La perpectiva axonométrica cumple dos propiedades importantes que la distinguen de la PERSPECTIVA CONICA:

• La escala del objeto representado no depende de su distancia al observador (equivalente a que el observador estuviera en el infinito).
• Dos lineas paralelas en la realidad son también paralelas en su representación axonométrica.

Perspectiva axonométrica: proporción de las medidas.

Los tres ejes del plano proyectante se dibujan así: el referente a la altura suele ser vertical, y los referentes a longitud y anchura pueden disponerse con cualquier ángulo. Los ejes del plano proyectante guardan entre sí 120º en la perspectiva asometrica, un caso particular de la perspectiva axonométrica. Si los ejes guardan entre sí 90º y 135º se denomina perspectiva caballera.

Para que el dibujo se parezca más a la realidad, se aplica a veces un coeficiente de reducción en las medidas paralelas a los ejes de anchura y longitud.

SISTEMA DIEDRICO

sistema dietrico

El sistema diédrico es un sistema de representación geométrico de los elementos del espacio sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyeccion ortagonal sobre dos planos que se cortan perpendicularmente. Para generar las vistas diédricas, uno de los planos se abate sobre el segundo.

Es un método gráfico de representación que consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces perpendiculares a dos planos principales de proyección, horizontal (PH) y vertical (PV). El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.

DIBUJO TECNICO

El dibujo técnico es un sistema de representación gráfico de diversos tipos de objetos con el fin de proporcionar información suficiente para facilitar su análisis, ayudar a elaborar su diseño y posibilitar la futura construcción y mantenimiento del mismo. Suele realizarse con el auxilio de medios informatizados o, directamente, sobre papel u otros soportes planos.

Los objetos, piezas, máquinas, edificios, planes urbanos, etc., se suelen representar en planta (vista superior, vista de techo, planta de piso, cubierta, etc.), alzado (vista frontal o anterior y lateral; al menos una) y secciones (o cortes ideales) indicando claramente sus dimensiones mediante acotaciones; son necesarias un mínimo de dos proyecciones (vistas del objeto) para aportar información útil del objeto.